The major calculation portion of this project is based around the concept of elementary cellular automation. Elementary cellular automation is used in many scientific fields of study including computability theory, mathematics, physics and theoretical biology. The basic theory behind elementary cellular automation is that each cell in a grid (for instance pixels on a screen) can be defined as either a “1” or a “0”. Given a particular starting state for each cell called “generation 0”. From this initial set, each pixel is defined to be in a new state by a set of governing rules that determine what each new generation of pixels will look like based upon the cells to the left and right of the cell in question, as well as the cell in question itself. The following illustration is an example of one of these rules. 1:
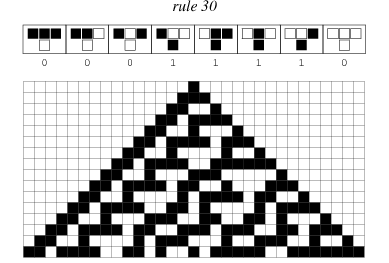
The graphic above the grid itself spells out a rule for each subsequent generation depending on neighboring states. This rule is called “rule 30” because the rule can be written as “00011110b” if white spaces are considered “0” and black are considered “1”, then this binary string is equal to 30 in decimal. With 2^8 possible strings that can be created with 8 spots for rule changes, there are 256 possible rules for elementary cellular automation.
Because Elementary Cellular automation only deals with 1D arrays, it may seem interesting that the results are in the form of a 2D array. This comes from the fact that we start with generation 0 as the top row, and each resulting automaton is layered beneath the previous generation. Instead of looking at the 2D array as a whole data set, it should be viewed as more of a timeline for the growth of the automation from its original generation 0 state, which in this case is a single black cell in the middle of the array.
While not every rule makes a distinct pattern to every other rule (there are actually only 88 unique rules), the patterns that they make are often very complex and vary in what actual uses that their results can be used for. For instance, rule 30 is used in Wolfram Alpha’s random number generator.
For more information on Elementary Cellular Automation, you can visit the links below:
http://mathworld.wolfram.com/ElementaryCellularAutomaton.html